Deconstructing Hashstack’s Dynamic Interest algorithm(DIAL)

Back in January 2021, when we first introduced the whitepaper for Open protocol, we intended to implement a savings apr that is at par with the savings interest offered by  the traditional financial(tradfi) institutions in high-growth economies; while also enabling a sense of predictable & stable apr. As we journeyed from the theoretical concept to an early prototype to the private testnet, this proposed solution underwent a series of  iterations.  Data suggested that high yield static interests could open up secondary risk vectors for the protocol; in particular, during the times of low-demand cycles. We went back to the drawing board to review the  interest model part of these efforts, we referred the algorithms used at Compound and Aave amongst other incumbent defi lending products. We tried to explore a fitment of the existing formulae with that of today's market practicalities. Unfortunately, none of the existing methodologies appeared reliable at-scale. This in conjunction with their inability to meet our specific needs to determine interest rates for each of the compartmentalised minimum commitment periods meant we needed to develop  an interest rate model that is derivative of the protocol's practicalities.

During our deliberation, we recognised the need for an autonomous, self-determining algorithm that factors in an asset's underlying supply-demand state while also considerate of various commitment periods. In this technical deep dive, we derive this algorithm. Note that, the interest rate model will continue to evolve with time to fit all practical challenges of tomorrow.

A mathematically self-determinant interest rate model considerate of various commitment periods.

As we dive into the Hashstack’s algorithmic interest rate model, [DIAL]; for ease, we have categorised the explanation in 4 parts.

1. Key variables, assumptions & premise.
2. Interest rate equation
3. Logic breakdown & deriving supply, borrow apr.
4. Caveats

Glossary

1. APR : Annual percentage rate
2. Liquidity provider:  Someone who provides liquidity to the protocol
3. Minimum commitment period[MCP]: A minimum time period for which a liquidity provider/borrower commits their liquidity/loans. MCP improves the protocols ability to predict the liquidity inward/outward.
4. Correlation factor: Used to determine the  strength of the relationship between the relative interest rates of two mcp.

Key variables, assumptions & premise

1. Minimum commitment period[mcp]: For Liquidity providers[None, Two weeks, One month, Three months]. For borrowers[None, One month]
2. APR range: For liquidity providers [0,15], borrowers[2,20]
3. Ur: Utilisation rate of an asset = Active loans / Total deposits. Ur is between 0 & 1; while the utilisation percentage, Up is between 0 & 100%. That is Up = 100 x Ur.

• Minimum annualized interest percentage  for liquidity providers is 0%[for all mcp].  Maximum is 15%[three month mcp].
• Minimum annualized interest percentage  for borrowers is 2%.  Maximum is 20%[1 month mcp].
• For liquidity providers, the correlation between 4 different mcp is as below.

• For borrowers, the correlation between 2 different mcp is as below.

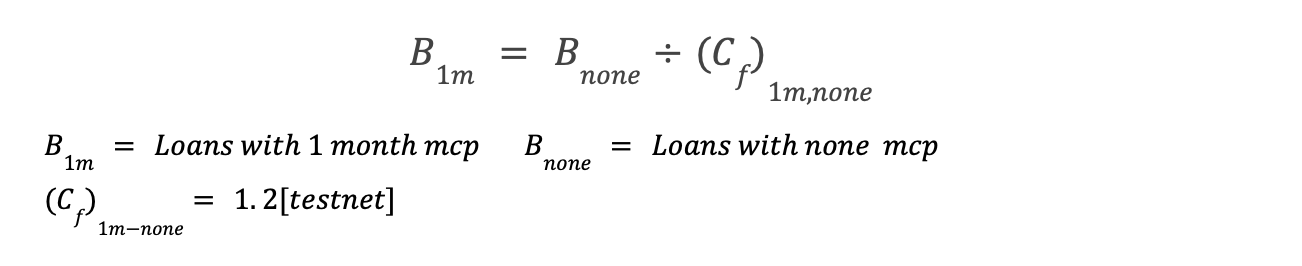
• The correlation factor between two adjacent mcp for both liquidity providers & borrowers is set to 1.2 during the testnet. However, this is configurable by the comptroller through the community governance/economist.
• Utilisation percentage(Up) is further classified into 6 ranges. This classification enables the interest model to insert eccentricity to the derived interest.

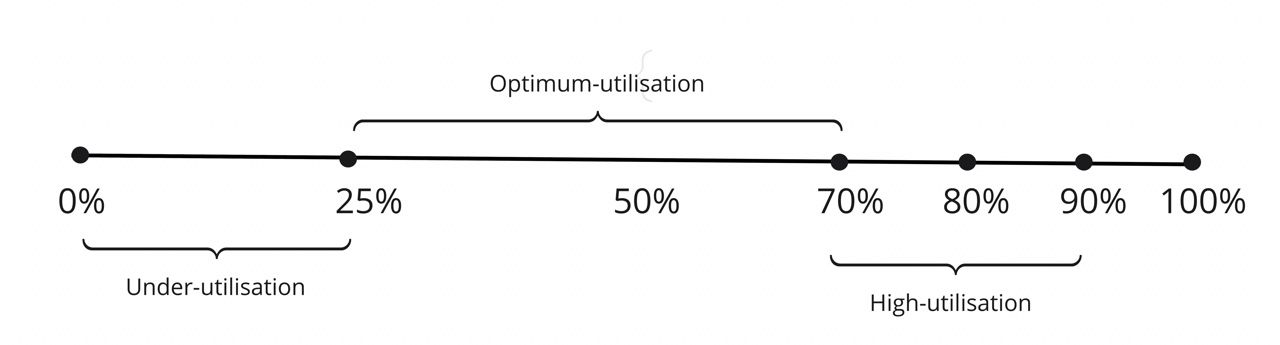
• Chainlink's verifiable random function[vrf]: Returns a random number from within the range of Utilisation percentage. This adds to a non-predictive estimated apr.

Interest rate equation

A self-sustainable interest model is the one that charges borrowers an apr just above the amount that needs to be repaid to its liquidity providers. The offset interest rate[i.e. difference between supply & borrow apr] enables the protocol to secure liquidity for insurance, and/or as rain-day fund. The below equation is our approach to a  a self-sustainable interest rate model.

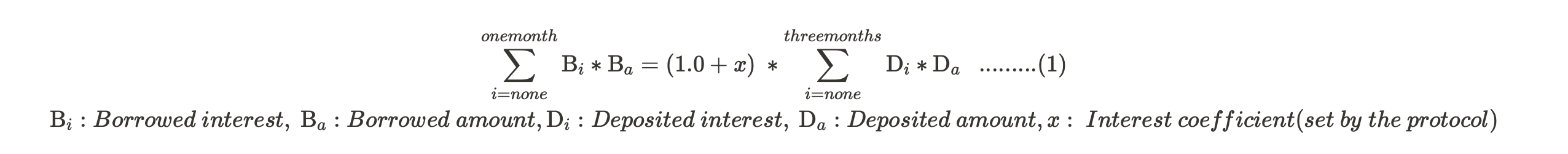
Simply put, the net apr charged to the borrowers should be just greater than the net apr to be paid to the liquidity providers. In the above equation, x is an offset factor which is expected to be between 0.5 to 1.5%. This offset provides a cushion to the protocol by charging the borrowers an apr that is effectively excess by a fractional percentage.

Logic breakdown, & deriving supply, borrow apr

To effectively determine payable interest rates, the dial model relies on the data points - effective asset utilisation, utilisation randomisation, deposits & loans by minimum commitment periods, and correlation between different commitment periods.

Let Utilisation percentage(Up)= 32%. This Up falls within the 25% to 50% Utilisation percentage classification. A random utilisation percentage is a random number between the classified range ( in this case, (25,50)). Open protocol relies on Chainlink vrf to determine a random number within a classified utilisation percentage range. For the sake of this explanation, let's assume the randomised utilisation as returned by vrf is 42. So, the dial uses 42% as utilisation percentage to calculate the supply & borrow apr.

This random utilisation percentage is converted into utilisation rate( Ur) by dividing it with 100. So, 42% becomes 0.42.

The Ur is then multiplied with the maximum supply apr; i.e. 0.15[15%]. We get 0.063. So, a liquidity provider with 3 months mcp is expected to be paid 0.063 x 100 = 6.3% apr against their savings at a randomised asset utilisation percentage of 42%.

15% apr is the maximum apr rewarded to the liquidity providers with 3 month mcp. The supply apr for the remnant mcp is determined by the correlation coefficient. For ease of this example, and as implemented in the testnet, it’s a flat figure of 1.2

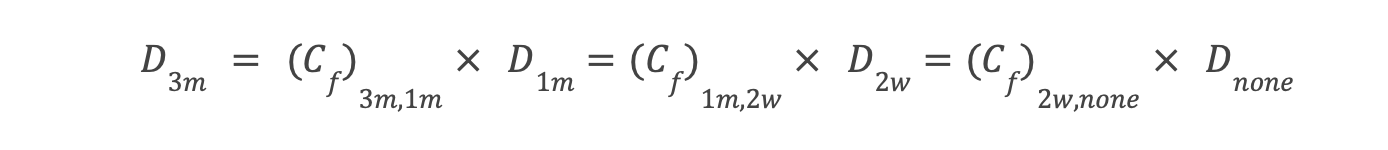
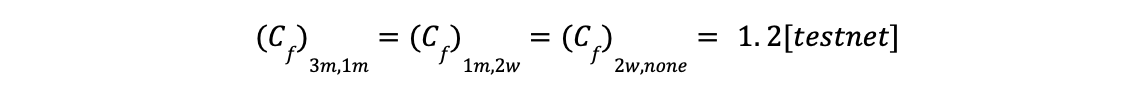
The supply apr for the remnant mcp thus derived is as follows :

1. D(1m) = 5.25%, or 0.0525 apr.
2. D(2w) = 4.375%, or 0.04375 apr.
3. D(none) = 3.645%, or 0.03645 apr.
   

This data is then fed into the primary equation,

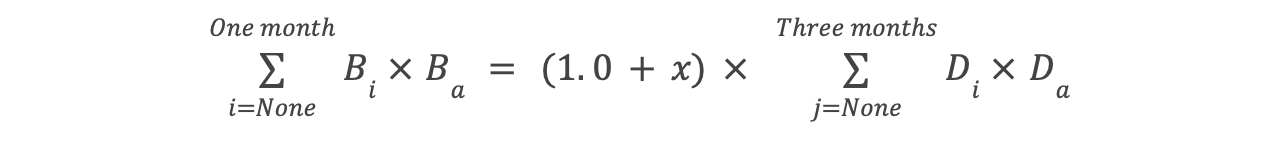
• Here, Da, i.e. deposit amount by mcp is known & can be fetched from the smart contracts. x = is an offset between 0.005 to 0.015; i.e. 0.5% to 1.5% set by the comptroller.
• Ba = Borrow amount by mcp. Known & can be fetched from the smart contracts.
• Di = Derived supply apr for each mcp.
• Bi = ?

Here we have 1 equation, and 1 unknown variable. The value of Bi can be easily determined. It can be denominated in 1month mcp, or none mcp using correlation coefficient as a basis. The borrow apr thus derived for a loan type of a specific mcp can be used to determine the borrow apr for another loan type using the correlation coefficient.

What if the derived borrow apr exceeds the permitted range of (2%, 20%)?

In such cases, the borrow apr is set to the maximum rate, i.e. 20% for 1 month mcp. From this, the borrow apr for none mcp is derived as 16.67%[i.e. 20%/1.2]. We use the below equation to calculate the apr for none mcp

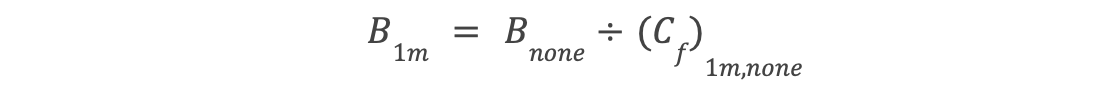
We add the borrow apr in the base equation.

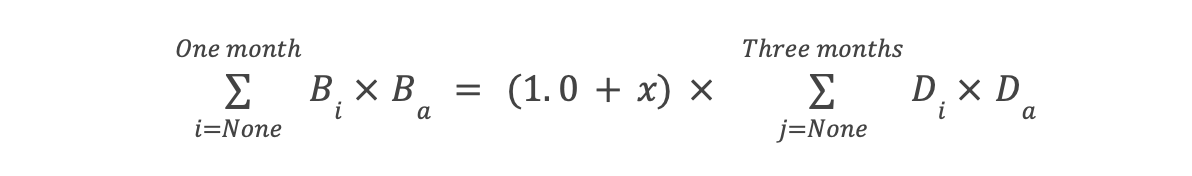
• Here, Da, i.e. deposit amount by mcp is known & can be fetched from the smart contracts. x = is an offset between 0.005 to 0.015; i.e. 0.5% to 1.5% set by the comptroller.
• Ba = Borrow amount by mcp. Known & can be fetched from the smart contracts.
• Bi = Derived borrow apr for each mcp
• Di = ?.

1 equation, and 1 unknown variable. The value of Di can be easily determined. It can be denominated in 3 month mcp, or none mcp. The supply apr for the remnant mcp can be easily determined basing the correlational factor as mentioned in this equation.

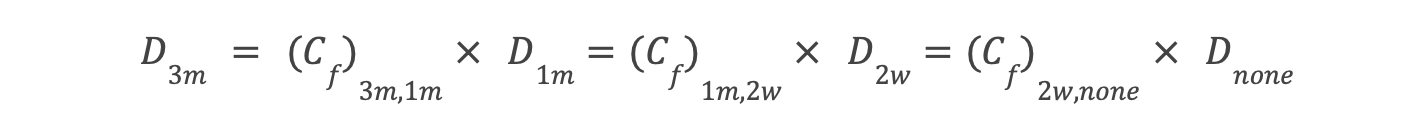
What if the derived supply apr exceeds the permitted range?

This is not possible. If you observe, in the first approach the supply apr determined was within the range min & max supply apr range; which could probably lead to a borrow apr exceeding the range. To maintain apr stability, the borrow apr is  then restricted to the maximum borrow apr as set by the comptroller. This effectively implies reducing the borrow apr. Since supply & borrow apr are directly proportional, the supply apr can only drop. Further, the supply apr can go as low as 0%. Thus, any supply apr derived through the reverse derivation will be well within the permitted range of supply apr.

Caveats

There are four caveats one should be aware of

1. Utilisation percentage ≤25%
2. Utilisation percentage ≥80%
3. Randomisation
4. Reserve factor.

When the asset utilisation is ≤25%, it indicates lack of market demand for the primary market in context. To rebalance supply-demand, the algorithm disincentives liquidity providers with a flat apr of 0% for assets with poor utilisation rate; while charges 2% apr for borrowers with none mcp.

When the asset utilisation is ≥80%, implying a high-demand asset, the supply & borrow apr will also be higher by the algorithm design. The algorithm in this particular context, incentivises liquidity providers with higher supply apr, which results in the derived borrowed apr to be higher as well, thus denoting the demand for the primary market. For assets with ≥80% utilisation percentage, 1% supply apr mark-up is added to the derived supply apr for 3 month mcp.

Open’s dial relies on randomisation at two points:

1. Randomising asset utilisation to a number within the utilisation range classification of that asset.
2. Randomising the interest calculation intervals [4 days to 7 days].

Randomisation introduces an anomaly intended to help the protocol mitigate liquidity manipulation by malefic entities who may add/remove liquidity just around the snapshot time to manipulate the apr.

The asset utilisation snapshot is taken at a random time of 4 to 7 days so as to build a sense of stable supply & borrow apr with restricted volatility.

Reserve factor -  A percentage of the total available liquidity locked from distributing as loans. This is set to 10% in the testnet. This means, 10% of the total deposits of a primary market is kept away from deployment as loans.

About Hashstack: Hashstack builds critical infrastructure necessary to further the usability of decentralised finance.

Open: Hashstack's solution to the over-collateralisation problem in defi lending, Open is a non-custodial money market protocol designed to enable secure under-collateralised loans on-chain.